# This is a chunk of R code. All text after a # symbol is a comment
# Set working directory using setwd() function
setwd('Enter the path to my working directory')
# Clear all variables in R's memory
rm(list=ls()) # Standard code to clear R's memoryA tutorial about data analysis using R (Website Version)
How to Read this Tutorial
This tutorial is a mixture of R code chunks and explanations of the code. The R code chunks will appear in boxes.
Below is an example of a chunk of R code:
Sometimes the output from running this R code will be displayed after the chunk of code.
Here is a chunk of code followed by the R output
2 + 4 # Use R to add two numbers[1] 6Objectives
The objectives of this tutorial are:
- Distinguish between the concepts of a sample and a population
- Introduce the concept of estimation and uncertainty in an estimate
- Explain the approach of bootstrapping to estimate a standard error
- Compare bootstrapping with classical statistical theory
Introduction
This tutorial looks at the use of a representativesampleto infer the central tendency of thepopulationfrom which the sample was taken.
We will look at the human height data from the HEIGHT.CSV data file. To start with we will import the data from the HEIGHT.CSV file and extract just the data for women from 2010 and 2011.
human = read.table('HEIGHT.CSV', header=T, sep=',') # Import human height data set
# Extract data for all females
humanF = subset(human, SEX=='Female')
# Extract data for females collected in 2010
humanF_2010 = subset(human, SEX=='Female' & YEAR==2010)
# Extract data for females collected in 2011
humanF_2011 = subset(human, SEX=='Female' & YEAR==2011) Before you continue:
Review this online lesson about sample and population.
Online Lesson:Sample and Population
This lesson is athttps://www.ucd.ie/ecomodel/OnlineLessons/lesson2_samplepopulation_Website.html
Population versus sample
To recap:
-
The topic of the question is calledthe populationand the data collected to answer the question is calledthe sample.
-
A sample rarely contains all the objects in a population. Therefore, the data you have available has information missing about the population (i.e. the objects for which you don’t have data).
The difference between a population and a sample is fundamental to understand if you want to use data to reliably say something about the world.
Data analysis is all about using a sample (partial data about the population) to makereliablestatements about the population.
The average height of a female US army recruit
Lets think about the concrete example of the HEIGHT.CSV data set.
Say we want to answer the question:
What is the mean height of female US army recruits?
The population
The population is the set of heights ofall womenwho have joined the US army.
The sample
We’ll use the data from 2010 (dataframehumanF_2010) as a sample. These data comprise 116 height measurements of army recruits. Whilst this is a decent amount of data it is still a small fraction of all the female recruits who have ever joined the US army.
The sample gives uspartial informationabout the population.
Estimating the mean of a population
If you had to guess how to estimate the mean of a population you may try using the mean of the sample. Congratulations! This would be a great guess. There is even statistical theory that supports using the mean of a sample.
Using the mean of our sample from 2010 gives us an answer to the question above:
Female US army recruits are 1.628 m tall on average.
But… we could have used the data from 2011 as the sample (dataframehumanF_2011).
Using the mean of data from 2011 gives us another answer to the question above:
Female US army recruits are 1.632 m tall on average.
We have two different answers! Which is the right answer?
The answer is that both answers are correct, allowing for someuncertainty.
Estimating uncertainty in the mean
Our estimates of the population mean have some uncertainty because the sample only givespartial informationabout the population.
To quantify the uncertainty in the estimated mean of the population mean we could
- take several samples,
- calculate the mean of each
- calculate the spread of these means. This spread will be a measure of uncertainty. Two common measures of uncertainty are:
- thestandard error of the mean: the standard deviation of the estimated means
- the95% confidence interval: the 2.5% and 97.5% quantiles of the estimated means
There’s a problem: sampling the population several times is nearly always going to be impractical and costly.
Thankfully there are solutions: methods have been developed to quantify uncertainty from a single sample. Here are two approaches.
Method 1: Bootstrapping
Bootstrapping is a very powerful technique that was originally proposed byEfron (1979). The idea is very simple: rather than resampling the population you resample the data you have, and then calculate the uncertainty in the means from these resamples. This approach turns out to be surprisingly good.
Bootstrap algorithm to estimate the uncertainty in a population's mean
===================================================
1. Resample the data set with replacement
2. Calculate the mean of the resampled data
3. Repeat steps 1 and 2 many times (e.g. 1000 times)
4. The standard deviation of the reampled means is an estimate of the standard error of the meanAside: There are several variation on the bootstrapping algorithm. The above algorithm is the percentile method. Puthet al.(2015)discuss the different bootstrap algorithms commonly used.
One way to bootstrap in R is to use thesample()function.
# Resample (with replacement) the numbers 1 to 10
sample(c(1:10), replace=TRUE) [1] 6 2 3 1 7 1 1 2 4 8There are 10 numbers that we are sampling . Thissample()command generates a new set of 10 numbers by randomly picking values from the original data. Thereplace=TRUEargument means that a single observation can be picked more than once (you can see that some numbers appear more than once in the resampled data). This is very important. Without thereplace=TRUEyour resample would be the same as the original data, which we don’t want.
# Resample (without replacement) the numbers 1 to 10
sample(c(1:10), replace=FALSE) [1] 3 6 9 8 10 4 1 2 5 7We can use thissample()command to generate a simple bootstrap estimate for the uncertainty in estimating the population mean. We will resample the 2010 data 10000 times.
# Code to perform a simple bootstrap for an estimate of the mean of a population
# Create a variable that will contain the means of the resampled data
resample_mean87 = array(NA, dim=10000)
# Use a for loop to resample the data 10000 times using 2010 data
for (i in 1:10000) {
resample = sample(humanF_2010$HEIGHT, replace=T)
# Save the mean of the resampled data in the array
resample_mean87[i] = mean(resample)
}
# Calculate the standard deviation of the resampled means
sd(resample_mean87)[1] 0.005537942Our bootstrap estimate for the standard error of the mean is 0.0055 m. Using this result we can now say that:
Female US army recruits are 1.628 +/- 0.006 m tall, on average.
We can do the same for the sample from 2011, which gives
Female US army recruits are 1.632 +/- 0.002 m tall, on average.
Now that we’ve estimated the standard error on the mean of our two means we can see that they are consistent to within the uncertainty.
As a rule of thumb: two estimates are consistent if the estimate’s uncertainties overlap (uncertainty must be measured by a 95% confidence interval or twice the standard error)
In this case, twice the standard error gives the ranges 1.617 - 1.639 m and 1.628 - 1.636 m. These two ranges overlap, indicating consistency in our estimates of the population.
The Sampling Distribution
Thesampling distributionis the distribution of means that we would estimate from many samples of a population. Our resampled means from the bootstrap give use an estimate of the sampling distribution. This sampling distribution can be visualise using a histogram.
# A histogram of the resampled means
hist(resample_mean87, n=50)
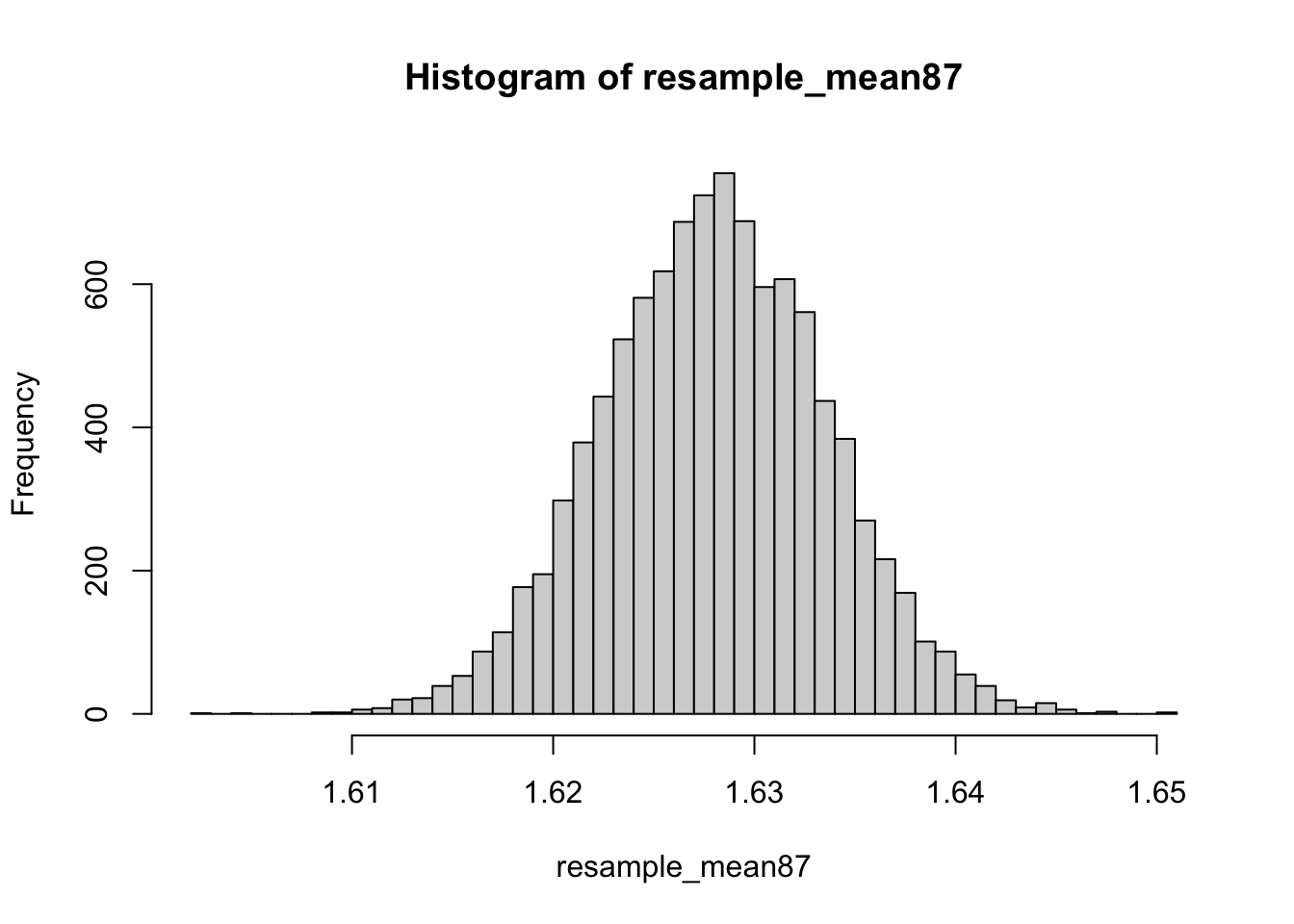
n theory, bootstrapping should work for many quantities (e.g. median, standard deviation, quantiles) not just the mean. Bootstrapping can even work on unusual estimates, such as evolutionary trees, or genetic sequence data.
However, bootstrapping is not always appropriate. For example, it should not be used to estimate uncertainties on extreme values (e.g. the maximum and minimum).
A range of different bootstrapping approaches exist, but are beyond the scope of this tutorial. R has a couple of packages to perform boostrapping (e.g. the packagesbootandbootstrap).
Bootstrapping is a very powerful tool.
Method 2: Statistical theory
A second approach to estimating the uncertainty in an estimated population mean is toassumethat a normal distribution can be used to approximate the population’s distribution of heights. This is an example of using a theoretical distribution (the normal distribution). My assuming a theoretical distribution is applicable we can make use of the statistical theory that underpins this distribution.
Assuming this normal distribution, then statistical theory tells us that
standard error of the mean≈sn−
where is the number of observations in your sample, and is the population standard deviation. Explaining how this formula is obtained is beyond the scope of these tutorials.
The formula says that as the sample size, , increases the uncertainty in the estimated population mean decreases. That makes intuitive sense: the more data you have, the more information your have and the less uncertainty there will be in your estimates.
Applying this formula to the height data for 2010 gives
# Calculate standard error of the mean from 2010
# using equation from statistical theory
n = nrow(humanF_2010) # The number of observations in humanF
sd(humanF_2010$HEIGHT) / sqrt(n) # Formula for the standard error of the mean[1] 0.005537021This approach gives a standard error of 0.006 m, in agreement with the bootstrap approach.
To use statistical theory you need to be confident that you are applying the correct formula. You need to know the result for
- the correct theoretical distribution (e.g. normal distribution)
- the correct quantity being estimated (e.g. the mean)
Summary of the topics covered
- A sample can be use to estimate properties of a population (e.g. mean, median)
- Using a sample to estimate a population has an inherent uncertainty.
- Bootstrapping is a powerful technique to estimate the uncertainty in using a sample to estimate a population
- Bootstrapping does not require the sample data to have a normal distribution
- Statistical theory can help to estimate the uncertainty in using a sample to estimate a population
- Statistical theory will make assumptions about the data (e.g. normal distribution)
- Increasing sample sizes estimate a population with increasing certainty.
Further Reading
All these books can be found in UCD’s library
- Graeme D. Ruxton and Nick Colegrave, 2010Experimental design for the life sciences, 3rd ed (Oxford University Press, Oxford)
- Michael J. Crawley, 2015Statistics : an introduction using R(John Wiley & Sons, Chichester) [Chapters 1, 5]
- Tenko Raykov and George A Marcoulides, 2013Basic statistics: an introduction with R(Rowman and Littlefield, Plymouth) [Chapters 7, 8]
- John Verzani, 2005Using R for introductory statistics(Chapman and Hall, London) [Chapter 5]
References
- Efron, B. 1979.“Bootstrap Methods: Another Look at the Jackknife.”Ann. Statist.7 (1): 1–26.(opens in a new window)https://doi.org/10.1214/aos/1176344552.
- Puth, Marie-Therese, Markus Neuhäuser, and Graeme D. Ruxton. 2015.“On the variety of methods for calculating confidence intervals by bootstrapping.”Journal of Animal Ecology84 (4): 892–97.(opens in a new window)https://doi.org/10.1111/1365-2656.12382.
